data set
- you have actually a data set which is organized into variables and you have cases.
- Each case is recorded for each variable
- If we do not have a data, we will not record that data.
- So, this is a tidy data set.
- Further, from data set you are able to look at the variables, you are able to broadly classify these variables as categorical variables and you are able to classify them as numerical variables.
- statistics means we want to learn from data.
- Now, when we want to learn from data the immediate thing is we want to see whether we can summarize this data.
Numerical Summaries
- When we say numerical summaries, we need to know whether we can do arithmetic operations on the data
- So, to know whether we can do arithmetic operations on data, we need to understand what are the scales of measurement
Scale Of Measurement
- when we look at scales of measurement, we have 4 scales of measurement and they are called the nominal, ordinal, interval and ratio scale.
Why is it important?
- It is extremely important for us to know what is the scale of measurement for each of the variables we have in my data set to eventually come up with what is the kind of summary we can do for that variable.
- Hence, it is extremely important for us to know what is the scale of measurement for each variable.
Nominal Scale
- When the data consists of labels or names, the scale of
measurement is considered a nominal scale.
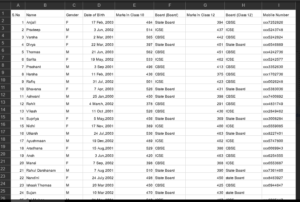
- Again, let us go back to our example.
- You can see in the first example we have name
which is evidently a nominal scale because it is only names, ok. - Again board you can see that it is labels in some sense we have a state board we have a ICSE, we have a CBSE,
- Whereas gender, again it is a label, we are labelling this category with a female and a male.
- So, you can see that names, board, gender.
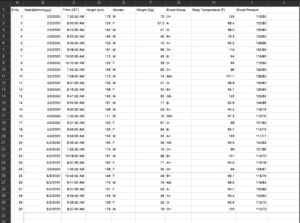
- We go back here, we have the blood data.
- In the blood group data you see again I can label it as O positive, A minus, O negative.
- One thing we need to notice here is we just have labels, we have only names; there is no particular order of these names.
- For example, the data would not have made any difference that is whether we are having a female male or a male female.
- So, this is the called a nominal scale of measurement.
- Sometimes we can see that nominal variables may be numerically coded.
What do we mean by a numerically coded nominal variable?
- For example, we have gender. Gender takes two labels which is male and female.
- we might code a male a 0 and a female a 1, we might code a male a 1 and a female is 0.
- So, this numerically coded is again equivalent to just labelling this variable, this numeric; no sanctity about having a 0 or a 1.
- we could label a man or 2 and woman a 3, or a woman a 5 and man a 7.
- All it says is this
- label has the same understanding; these numbers have no meaning when you are coding
the nominal variables. Both the codes are valid that is what we mean. - When no nominal variables are coded whether 1 or 2 or 3 and 1, it has both codes are valid.
- There is no ordering.
- This is extremely important that we understand when we talk about nominal variables; there is no ordering in the variable.
- So, a nominal variable is just name categories without implying order.
Three data set
- Going back to a data sets in the student data set, name, gender, board are nominal variables.
- In a blood bank data set, we have gender and blood group which are nominal variables.
- In the cricketing data set jersey number is a nominal variable.
- The role of batsman is a nominal variable, that is and the player name is a nominal variable.
- So, nominal scale of measurement is used when we have name categories without implying any order.
Ordinal Scale
- The next scale of measurement is called an ordinal scale of measurement where the data exhibits the same property of nominal data, but here an order or rank is meaningful.
- For example, a customer who visits a restaurant provides a service rating of excellent good and poor.
- The data are again labels.
- For example, we can have a data where we have customer 1 who gives a rating of excellent, customer 2 good, customer 3 bad, customer 4 again good.
- So, if you look at the variable, the variable is rating.
- Here you can again see this is taking a nominal value.
- By nominal it is taking a categorical value where my categorical variable has 3 categories; excellent, good and
bad, but within this categorical variable there is an order. - You know the order is bad, good and excellent.
- So, categorical or nominal data which exhibit some rank or an order or rank is meaningful is said to have the measurement, the scale of measurement is said
to be a ordinal scale. - So, ordinal scale of data is name categories that can be ordered.
interval scale of measurement
- The next scale is called an interval scale of measurement.
- When we talk about ordinal scale, again we can code an ordinal scale of measurement.
- For example, in our earlier example my bad could have been coded as 1, my good can be coded as 2, and my
excellent can be coded as 3. - we could code them.
- There is an order in 1, 2, 3.
- But then one thing which we need to understand here is the distance between bad to good need not be the same as the distance between good and excellent.
- It is just an order, we know excellent is better than good, but we cannot say that excellent the difference between good and excellent is the same as the distance between good and bad.
- we have an order, but at this point of time we am not able to comment anything more about this order.
- So, when we go to interval scale of data, interval scale of data has all the properties of interval scale of data, but the interval between the values is expresses a fixed unit of measure.
- when we have internal data we have an ordering, but in this case whenever we are ordering my data the interval between the values is expressed in units of a fixed unit of measure.
- Now, here ratios do not have any meaning because the value of 0 is arbitrary.
- Let usexplain this through an example. Interval data and numerical values that can be added or subtracted, it has no absolute 0.
- Let us look at temperature as an example.
- Suppose, the reference or response to a question is how hot the day is, and you respond as just comfortable uncomfortable or just good, bad.
- we are just giving a label to my feeling.
- we are not grading or ordering this feeling we have, whether we are just telling it is comfortable it is categorized into comfortable and uncomfortable or it could be just leisurely or the something.
- Temperature is a variable of interest and here you can see temperature is a nominal variable.
- Now, suppose temperature is again the variable of interest, but here we am interested in knowing how hot a liquid is, whether it is cold, warm, or hot; you see that there is a order in this variable.
- we know cold has warm is warmer than cold or hot is warmer than warm, the variable is ordinal.
- However, here we do not know whether the difference between a warm and a cold beverage is the same as a hot and a warm beverage.
- But now suppose I am measuring the temperature, consider an AC room which is set at 20 degree centigrade and temperature out of their outside the room is 40 degree centigrade it is correct to say that the difference in the temperature is 20 degree centigrade, absolutely fine.
- we had set it at 10 degree, 14 degree centigrade and the temperature outside was 28 degrees, it is perfectly right for me to tell that there is a difference in the temperature of 14 degree centigrade.
- But it is incorrect; it is absolutely incorrect for me to say that outdoors is twice as hot as indoors because 40 degree centigrade is not twice as hot as 20 degree centigrade.
- when we are able to; so, that tells me that we can talk about the difference between any two values, but here ratios have no meaning.
Temprature
- Again, we understand from temperature, at least when we talk about Celsius and Fahrenheit scales there, there is no absolute 0, in the Celsius 0 and 100 are set to be as
the freezing point and the boiling point whereas, in Fahrenheit it is 32 and 212. - Only in the Kelvin you have a 0 degree, where 0 means absolutely no temperature.
- But when you are talking about Celsius and Fahrenheit we understand that there is no absolute 0.
- So, when you talk about an interval scale, it is extremely important for us to understand there is no absolute 0.
- However, the difference between an interval scale and an ordinal scale of measurement is in an interval scale the difference between the values is fixed unit of measure whereas, for a ordinal scale that need not be a fixed unit of measure that is good to bad need not be the same difference as excellent to good
- This is the key difference.
ratio scale of measurement.
- In a ratio scale of measurement it has all properties of interval data and the ratio is a very meaningful measure.
- The scale is a ratio scale.
- So, the example, height, weight, marks.
- Like I know a person who has scored 300 has scored twice as well as a person who has scored 150 marks.
- So, we can have a notion of a ratio which we can define here, the variables, height, weight, marks, runs, wickets all of them are examples of ratio scale of measurement.
- So, ratio when you have a variable which is measured in the ratio scale; you can do all the mathematical or arithmetic operations on it.
- You can add, you can subtract, you can multiply or divide.
- Whereas, when you talk about interval scale you can only talk about difference or you can add and subtract.
- You have no absolute 0, so ratios do not have any meaning.
Summary
- Whenever you are presented with the data set after you identify the variables as categorical or numerical, it is extremely important for us to understand that when we have categorical data, we have the nominal and ordinal scale.
- Within the nominal scale, we have nominal which is only named category, ordinal is a name with an order.
- Here the difference between order is not a fixed measure.
- Again, example for categorical data name, blood group or nominal scale; ordinal scale ranking, rating; there is a order, but then there need not be a fixed order in the rating.
- Absolute 0 does not exist for an interval scale.
- This is for numerical data or quantitative
data. - Absolute 0 does not exist, but proportional difference exists.
why are we interested about the scales of measurement?
- In nominal no arithmetic operations possible.
- In Ordinal scale we have some sense of an order.
- In internal scale we do addition, subtraction.
- In ratio scale we can do all arithmetic operations.
- For example, when I have a variable which is a blood group I would not be asking the
a data set which is very well organized, identify variables as categorical or numerical. And once you are able to identify these variables further look at what are the scales of measurement whether it is a nominal, whether it is an ordinal scale of measurement or whether it is an interval scale of measurement or ratio scale of measurement. There is a
difference, and the critical difference is in an interval there is no absolute 0, whereas in a ratio scale an absolute or a true 0 exist.