Set Theory | StudyTution

What is the set?

A set is the collection of items.
R denotes the Real numbers.
Real number includes all the rationals, fractions, but also numbers that con not be represent as fractions, such as the squre root of 2and other irrationals numbers like pi and e.
Mathematically there is no constraint on the requirement that members of a set have uniform type.
A set can have any kind of numbers, even a mixed membership; there is no uniformity of type.

Difference between a set, sequence or a list

The difference is that the order in which we identify a set does not matter.
When we talk of numbers, we tend to list them in a particular way but as the set it does not matter.
So, the sequence does not matter what matter is that if we happened to accidentally write the same number twice it does not change the set.

Cardinality

The cardinality of a set is the number of items in the set and if it is a finite set we can count them.
The set of regular polygon is infinite.
The corresponding notion to a regular polygon is what is called a platonic solid.
In a platonic solid, first of all we have surfaces or sides each sides is a regular polygon and all these regular polygons meet at the same angles in three dimensions.
There are only 5 plantonic solids in three dimensions.
So, this is an example of a set which turns out to be finite, even though there is no reason for it to be finite.

5 Plantonic Solids

The tetrahedron which has triangles.
The cube which has square.
Octahedron which has 8 sides which ae triangles.
Dodecahedron with 12
Icosahedron with 20 sides.
We are adding things to the integers to get rational numbers.

How do we describe a set

We use curly bract and commons for finite set.

Bertrand Russell

Bertrand Russell show that there is a problem if we collect all the sets together and call it a set.
So, if we have a set of all sets, then we have a problem and this is something which is called Russell Paradox.
Though the notion of a set is intuitive and it seems natural that any collection of objects is a set, we have a actually be a little careful in maths, if we are using sets in order to define what is a set and what is not a set.

Elements

The most formal notation for the memebers of a set is an element.
So, a set consist of elements and we write ths membership of an element in a set using this e notion ( ∈ ).
So, when we write x∈X, it means that small x is an element of X.

Subsets

When one set is included in other set the this is called subset.
X is a subset of Y, if every element of X is also an element of Y and this is written as ⊆ subset notaion.
Since, natural numbers are included in the integers so, N is a subset of Z.
As we extended Z to Q so, the set of integers is a subset of the rational and the set of rational is a sunset of reals.
Every set is a subset of itself because every element of X is also an element of X.
Two sets are equal if and only if, they are actually the same sets of elements.
To check this, one way is that check everything in the first set belongs to the second set.
So, X is a subset of Y and everything in the second set belongs to the first set.
So, Y is subset of X.
We use ⊆ for when we want to say that it is a subset, but it is actually equal.
As we know that natural number is a subset of the integers because the negative numbers are not there.
Integers are clearly a proper subset of the rationals and because the irrationals numbers are not rational, the rational are a proper subset of the real numbers.

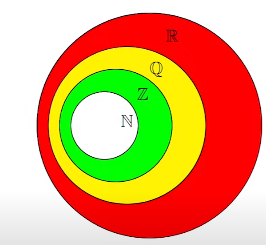
Venn Diagram

It is useful to picturize a set and relationships between sets; is one a sebset of another, is one set not a subset of another and so on.
We use Venn Diagram pictorially in order to represent sets.

Empty Sets

Its is the set with no elements.
The notation for the empty set is ∅
The empty set is actually a subset of any set.
The vacuous statement are called for the sentence which use the word all where the set is empty.
So, in particular, every element of the empty set because there are none.
If we puta brace around the empty set then we create a set with one element.

Power Subset

When we group the subset of a set into a larger set, then we get the powerset.
The power set of the empty set is a set consisting of just one element, namely the empty set itself.
The empty set on its own denotes a set with no elements, but an empty set with a brace around it is not the same thing.
It is a set consisting of one element, namely the empty set
if we have two elements, then the power set had four elements.
So, in fact, one can generalize this and say that if we have n elements, then we would have 2 to the n subsets.
So, for instance, if we had a, b, c right, then we would have 1 subset which is empty.
We would have 3 subsets which are one element each and then, we would have 3 more subsets which are 2 elements each a, b a, c and b, c and finally, we would have the set itself right.
So, these are the only subsets.
If you add these up, this is 8 which is 2 to the power 3.

why is it that a set with n element should have 2 to the n subsets, no more no less?

Supposing we have n elements in the set.
So, let us just call these without describing what they are specifically as x 1, x 2 up to x n.
So, we have n distinct elements x 1 to x n.
Remember these must be different because you cannot duplicate elements in the set .

how do you construct a subset?

Well for each element X i, we have to either include the set include X i in the subset or exclude X i subset.
So, we have to make a choice for each X i right.
overall, we have to make n choices right.
For each X i, we have to decide whether to include it or exclude it from the subset.
We are we have two different choices for each elements.
we have two ways to decide whether to do something with x 1, keep it or leave it; x 2 keep it or leave it.
then we have two times two choices for x 1 and x 2 together; two times two times two choices for x 1, x 2, x 3 together.
in general, if we have n such choices where each choice involves two options, then we have 2 into 2 into 2, n times 2 to the power n choices .
each of these choices gives us different subset.
whenever we make a different choice, we will either leave out i from the set or put an X i.
So, it will differ from the choice, where we do the other thing .
So, each choice generates a separate subset.
So, there are exactly 2 to the n subsets .

Another way of looking at subsets and getting to the same result .

Subset and binary numbers

we can actually think of subsets in terms of binary numbers .
So, let us again think of our n element set x 1 to x n right.
now, supposing we look at n digit binary number.
So, digit actually is comes from decimal. So, we say bit for binary digit.
So, n bit binary number.
So, remember in a binary number system, we have 0’s and 1’s and the place values represent powers of two. . So, we have the unit digits is units as usual.
The next digit 2 to the power 0 is a is number of twos, number of fours, number of eights.
So, it is like the decimal thing is in base 10.
This is in base 2 .
So, now, if we look at n bit binary numbers, then for instance, if we look at 3 bit binary numbers, then we have 8 of them.
We can start with 0 0 0, then 0 0 1, 0 1 0 and so on up to 1 1 1 and again, the reason that there are 2 to the n, n bit numbers is because for each bit we can choose to put 0 or 1.
So, we have two choices for the first bit, two choice for second bit and so on.
So, it is not surprising that an n bit binary number can represent 2 to the n different values from 0 to 2 to the n minus 1, if we think of them as numbers .
we will look at is the ith bit and say that the ith bit represents the choice that we made.
If we chose to keep X i in our subset, we will call it 0.
If we chose to we will call it 1 for example.
And if we choose o omit X i from our set, we will call it 0.
So, 0 represents the choice, where we leave out X I; 1 represent the choice, where we keep X i.
supposing we have this four elements set a, b, c, d; then, if we look at the binary sequence or the bit sequence 0 1 0 1, the first 0 corresponds to a, so it says leave out a.
The second 0 corresponds to c, so it says leave out c and for b and d we have put a 1.
So, it says keep b and keep b.
So, it says leave out a, keep b, leave out c, keep d .
So, this 0 1 0 1 as a binary sequence corresponds to the set b comma d .

What does 0 0 0, the all 0 sequence say?

The all 0 sequence says every X i in the set is omitted from the subset .
So, this is precisely the subset which is the empty set because it has no elements

what about the all 1 sequence?

the all 1 sequence says every X i that we have is included in the final subset .
This is the set itself.
These are the two extreme subsets; the empty set and the set itself and all the other ones come in between .
So, from this, we can see that every n bit number represents one sequence of choices. So, this gives us 2 to the n choices because there are precisely 2 to the n, n bit numbers.
any finite set with n elements has exactly 2 to the n subsets.

Facebook Comments Box